2D Range Sum
2D Range Sum
Problem
Solution
Naive 2D DP precaculation solution (4148 ms)
"""
runtime: 4148 ms
Time complexity: O(n^3)
Space complexity: O(n^2)
"""
class Solution:
def maximalSquare(self, matrix: List[List[str]]) -> int:
if not matrix or not matrix[0]:return 0
R, C = len(matrix), len(matrix[0])
dp = [[0]*(C+1) for _ in range(R+1)]
for i in range(R):
for j in range(C):
dp[i+1][j+1] = dp[i][j+1]+dp[i+1][j]-dp[i][j]+int(matrix[i][j])
res = 0
for i in range(R):
for j in range(C):
for k in range(i, R):
d = k - i
new_j = j + d
if new_j<C:
if (d+1)**2>res and dp[k+1][new_j+1]-dp[k+1][j]-dp[i][new_j+1]+dp[i][j]==(d+1)**2:
res = (d+1)**2
return res
A better one (200 ms)
A better one can be found here. Below two images are from here.
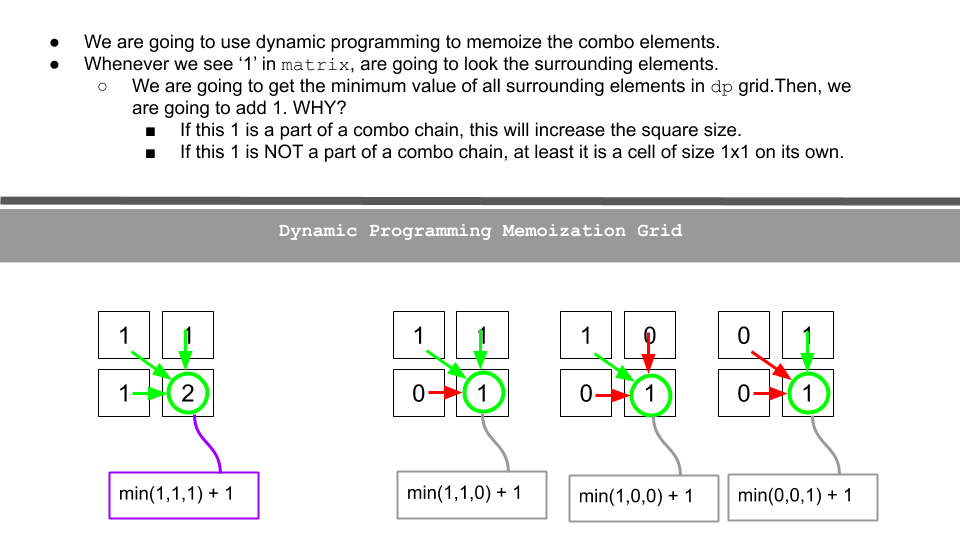
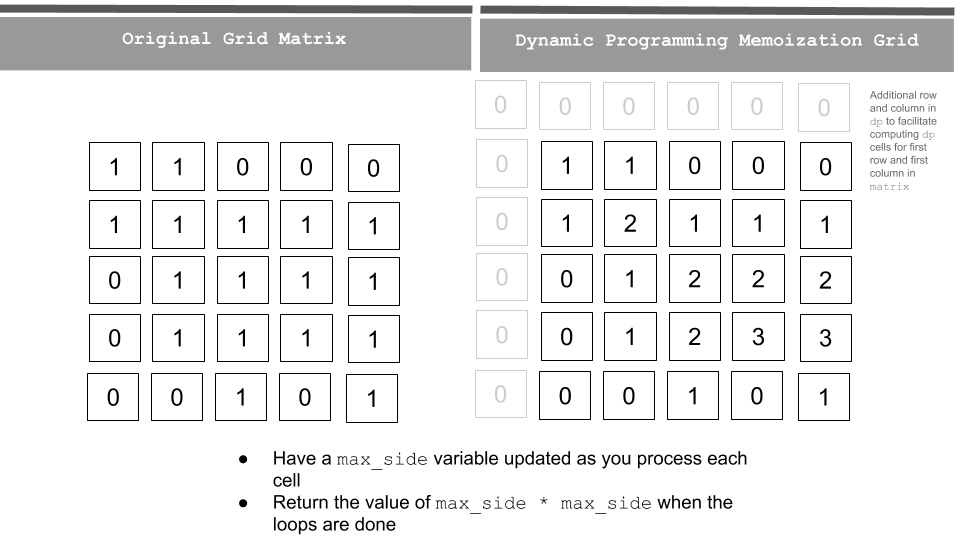After you read the original post, and the code should be straightforward.
# time complexity: O(mn)
# Space complexity: O(1)
class Solution:
def maximalSquare(self, matrix: List[List[str]]) -> int:
if not matrix or not matrix[0]:return 0
R, C = len(matrix), len(matrix[0])
res = 0
for i in range(R):
for j in range(C):
if i==0 or j==0:
matrix[i][j] = int(matrix[i][j])
res = max(res, matrix[i][j])
else:
if matrix[i][j]=='1':
matrix[i][j] = min(matrix[i-1][j], matrix[i-1][j-1], matrix[i][j-1])+1
res = max(res, matrix[i][j])
else:
matrix[i][j] = 0
return res**2
Thanks for reading.